反向传播:神经网络训练的基石
大模型开发/技术交流
- LLM
10月23日150看过
引言
反向传播算法是深度学习模型训练中不可或缺的计算技术,它使得模型训练在计算上变得高效可行。在现代神经网络中,反向传播能够将梯度下降的训练速度提升大约一千万倍。
反向传播的应用不仅限于深度学习领域,它还是一个强大的计算工具,广泛应用于天气预报、数值稳定性分析等多个领域,尽管在这些领域它可能以不同的名称出现。事实上,这个算法在不同领域被独立发明了数十次(参见 Griewank (2010))。在更广泛的背景下,它被称为“反向模式微分”。
本质上,反向传播是一种快速计算导数的技术。无论是在深度学习还是其他数值计算场景中,掌握这一技巧都是至关重要的。
计算图


这种图在计算机科学中十分常见,尤其是在函数式编程的讨论中。它们与依赖图和调用图的概念密切相关,并且是流行的深度学习框架Theano的核心抽象。
我们可以通过为输入变量赋予特定值,并沿着图计算节点来评估表达式。例如,设置 a=2和 b=1


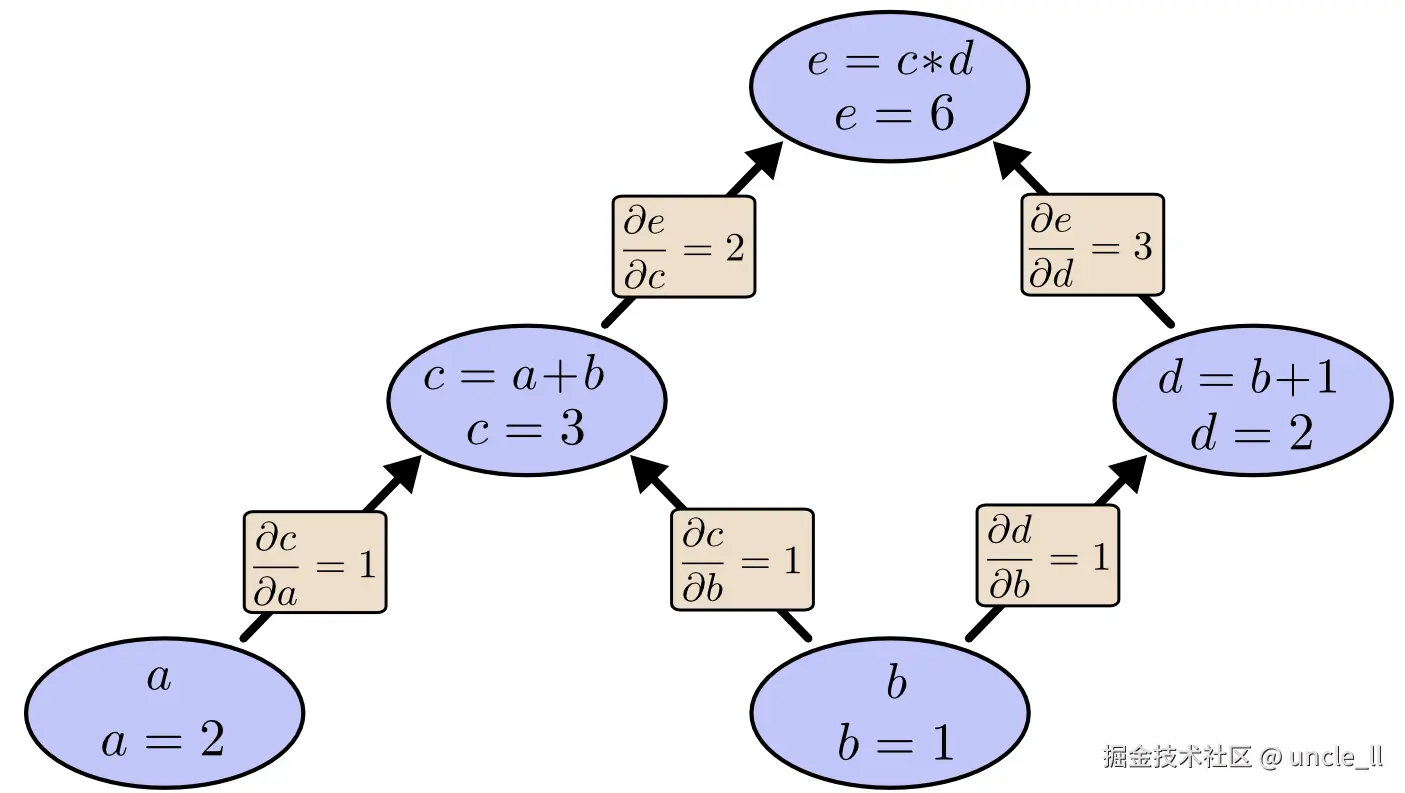

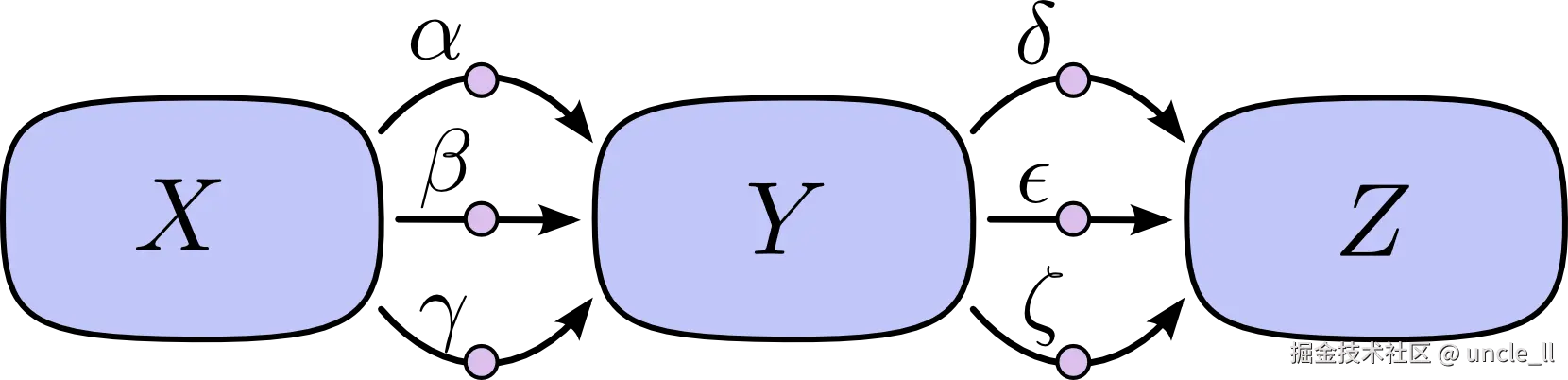

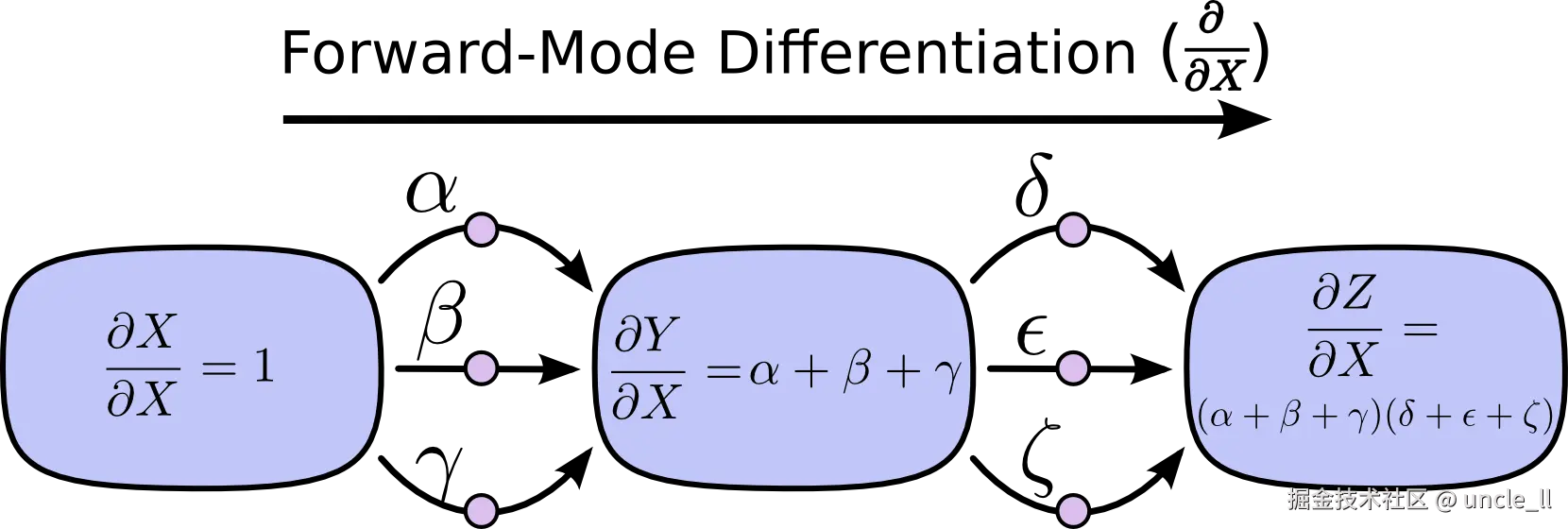
如果你上过微积分课程,可能会发现前向模式微分与你学到的内容非常相似,尽管你可能没有从计算图的角度考虑过。
另一方面,反向模式微分则从图的输出开始,向输入端移动。在每个节点,它合并所有从该节点出发的路径。

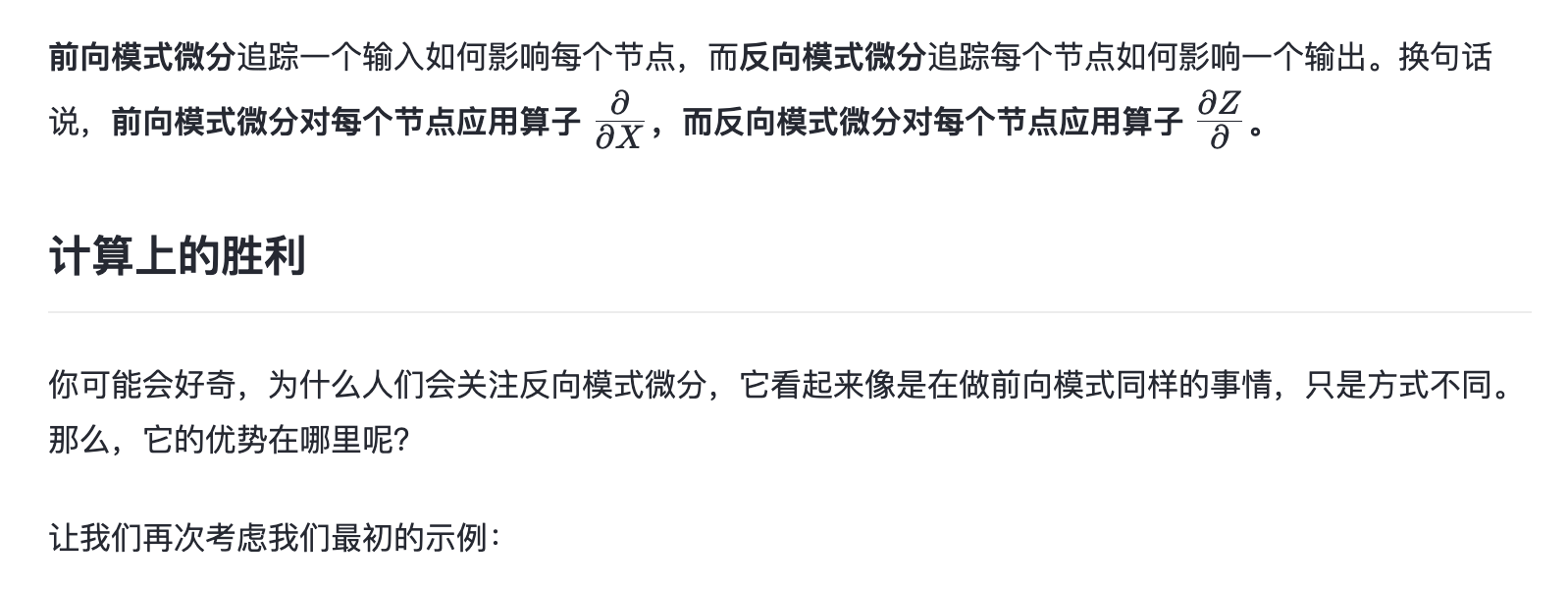

使用从
b 开始的前向模式微分,我们可以得到每个节点相对于 b 的导数。





工作原理
-
计算图:首先,将计算过程表示为一个计算图。计算图是一系列计算步骤的图形表示,其中的节点表示变量,边表示操作。
-
正向传播:在正向传播阶段,计算图从输入到输出执行计算,计算图中每步的结果。
-
计算导数:在前向模式微分中,同时计算每个操作的局部导数(或雅可比矩阵),并将这些导数沿着计算图正向传播,直到达到输出。
-
累积导数:在传播过程中,每个节点的导数会累积前一步的导数和当前操作的局部导数。
特点
-
效率:对于每个输入变量,前向模式微分可以一次性计算出输出相对于该输入的导数。这对于少量输入变量的情况非常高效。
-
适用性:当模型的输入参数数量远小于输出维度时,前向模式微分通常比反向模式微分更高效。
应用场景
-
神经网络训练:在神经网络中,前向模式微分可以用于计算网络输出相对于每个输入的梯度,这在某些特定的应用场景中非常有用,比如当需要对输入数据进行调整以优化输出时。
-
符号计算:在符号计算库中,前向模式微分被用来计算表达式的梯度,这在数学和物理问题的解析解中很常见。
反向模式微分
反向模式微分(Reverse Mode Differentiation)是一种在计算图中从输出向输入方向计算导数的方法。这种方法在深度学习和神经网络训练中尤为重要,因为它允许高效地计算损失函数相对于网络参数的梯度,这是梯度下降和其他优化算法的基础。
工作原理
-
计算图:首先,将计算过程表示为一个计算图。计算图是一系列计算步骤的图形表示,其中的节点表示变量,边表示操作。
-
正向传播:在正向传播阶段,计算图从输入到输出执行计算,计算图中每步的结果。
-
反向传播:在反向模式微分中,我们从输出开始,反向计算输出相对于每个参数的导数。这个过程遵循链式法则,每一步的导数计算依赖于前一步的结果。
-
累积梯度:在反向传播过程中,每个节点的梯度会累积前一步的梯度和当前操作的局部导数。
特点
-
效率:反向模式微分特别适用于神经网络,因为神经网络通常有大量的参数和相对较少的输出。这种方法可以一次性计算所有参数的梯度,从而减少了计算资源的消耗。
-
适用性:当模型的参数数量远大于输出维度时,反向模式微分比前向模式微分更高效。
应用场景
-
神经网络训练:在神经网络中,反向模式微分用于计算网络输出相对于每个参数的梯度,这对于训练过程中的参数更新至关重要。
-
梯度计算:在机器学习中,反向模式微分是计算梯度的基本工具,用于优化模型参数以最小化损失函数。
效率对比
-
前向模式微分:如果函数有
n个输入和m个输出,前向模式微分需要 O(n×m)O(n \times m)O(n×m) 的计算量来计算雅可比矩阵。 -
反向模式微分:如果函数有
n个输入和m个输出,反向模式微分只需要 O(n+m)O(n + m)O(n+m) 的计算量来计算梯度向量。
选择前向模式微分还是反向模式微分取决于具体问题的需求。在大多数深度学习应用中,由于模型参数的数量通常远大于输入数量,反向模式微分是首选方法。然而,在某些特定的优化问题或当需要计算雅可比矩阵时,前向模式微分可能更合适。理解这两种方法的差异对于选择合适的自动微分策略至关重要。
反向传播和前向模式微分展示了如何通过线性化和动态规划等技巧来高效计算导数。理解这些技术可以帮助我们更有效地计算涉及导数的其他表达式。
反向传播不仅是一种计算工具,它还提供了一个视角,帮助我们理解导数在模型中的流动方式,这对于解决某些模型难以优化的问题至关重要,如循环神经网络中的梯度消失问题。
参考
————————————————
版权声明:本文为稀土掘金博主「uncle_ll」的原创文章
如有侵权,请联系千帆社区进行删除
评论
