机器学习|深度学习基础知识

大模型开发/技术交流

12月2日323看过

最近在看深度学习的一些资料，发现有些基础知识比较模糊，于是重新整理了一下深度学习的基础知识。

1、基础知识

1.1 神经元

神经元是生物学的概念，神经网络的基本组成单元，神经元细胞有兴奋和抑制两种功能，当神经元接受到的信号超过阈值时，就会产生兴奋，否则就产生抑制。

在计算机模拟下，神经元可以接受多个输入信号，经过加权和运算后，输出一个结果。

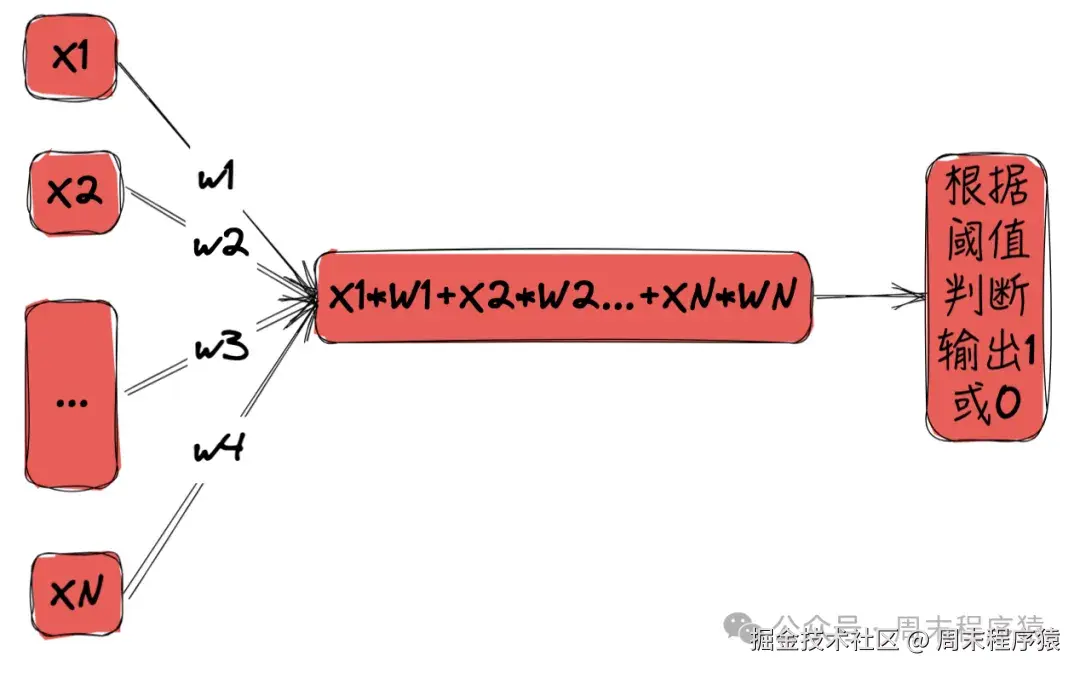
神经元

给定N个输入信号，每个信号的权重为w1, w2, ..., wN
将信号和权重做线性计算，得到线性计算结果：x1w1 + x2w2 + ... + xN*wN
获得的值与既定阈值比较，如果大于阈值，则输出1，否则输出0
这样就能确定当前神经元处于兴奋还是抑制状态，如果处于兴奋状态就往后传递，否则就停止传递

1.2 单层感知机

1957年 Frank Rosenblatt 提出了一种简单的人工神经网络，被称之为感知机。

其实早期的单层感知机和神经元很相似，都是接受多个输入信号，经过加权和运算后，输出一个结果，唯一的区别是增加偏置项，通过偏置项，可以控制神经元处于兴奋还是抑制状态，其计算公式如下：

  
  
  
  
  
  
   
   
   
   
   
   
    f(x) = sign(w1*x1 + w2*x2 + ... + wn*xn + b)

通过numpy实现样例代码如下：

  
  
  
  
  
  
   
   
   
   
   
   
    import numpy as np  
   
   
   
   
   
   
   
   
   
   
   
   
      
   
   
   
   
   
   
   
   
   
   
   
   
    class Perceptron:  
   
   
   
   
   
   
   
   
   
   
   
   
        def __init__(self, learning_rate=0.01, n_iters=1000):  
   
   
   
   
   
   
   
   
   
   
   
   
            self.lr = learning_rate  
   
   
   
   
   
   
   
   
   
   
   
   
            self.n_iters = n_iters  
   
   
   
   
   
   
   
   
   
   
   
   
            self.activation_func = self._unit_step_func  
   
   
   
   
   
   
   
   
   
   
   
   
            self.weights = None  
   
   
   
   
   
   
   
   
   
   
   
   
            self.bias = None  
   
   
   
   
   
   
   
   
   
   
   
   
      
   
   
   
   
   
   
   
   
   
   
   
   
        def fit(self, X, y):  
   
   
   
   
   
   
   
   
   
   
   
   
            n_samples, n_features = X.shape  
   
   
   
   
   
   
   
   
   
   
   
   
      
   
   
   
   
   
   
   
   
   
   
   
   
            np.random.seed(1)
   
   
   
   
   
   
   
   
   
   
   
   
            # 初始化权重为小的随机值，偏置为0  
   
   
   
   
   
   
   
   
   
   
   
   
            self.weights = np.random.random(n_features) * 2 - 1
   
   
   
   
   
   
   
   
   
   
   
   
            self.bias = 0  
   
   
   
   
   
   
   
   
   
   
   
   
      
   
   
   
   
   
   
   
   
   
   
   
   
            y_ = np.array([1 if i > 0 else 0 for i in y])  # 将标签转换为0和1  
   
   
   
   
   
   
   
   
   
   
   
   
      
   
   
   
   
   
   
   
   
   
   
   
   
            for _ in range(self.n_iters):  
   
   
   
   
   
   
   
   
   
   
   
   
                for idx, x_i in enumerate(X):  
   
   
   
   
   
   
   
   
   
   
   
   
                    linear_output = np.dot(x_i, self.weights) + self.bias  
   
   
   
   
   
   
   
   
   
   
   
   
                    y_predicted = self.activation_func(linear_output)  
   
   
   
   
   
   
   
   
   
   
   
   
                    update = self.lr * (y_[idx] - y_predicted)  
   
   
   
   
   
   
   
   
   
   
   
   
                    self.weights += update * x_i  
   
   
   
   
   
   
   
   
   
   
   
   
                    self.bias += update  
   
   
   
   
   
   
   
   
   
   
   
   
      
   
   
   
   
   
   
   
   
   
   
   
   
        def predict(self, X):  
   
   
   
   
   
   
   
   
   
   
   
   
            linear_output = np.dot(X, self.weights) + self.bias  
   
   
   
   
   
   
   
   
   
   
   
   
            y_predicted = self.activation_func(linear_output)  
   
   
   
   
   
   
   
   
   
   
   
   
            return y_predicted  
   
   
   
   
   
   
   
   
   
   
   
   
      
   
   
   
   
   
   
   
   
   
   
   
   
        def _unit_step_func(self, x):  
   
   
   
   
   
   
   
   
   
   
   
   
            # 单位阶跃函数，用于二分类问题  
   
   
   
   
   
   
   
   
   
   
   
   
            return np.where(x >= 0, 1, 0)  
   
   
   
   
   
   
   
   
   
   
   
   
      
   
   
   
   
   
   
   
   
   
   
   
   
    # 示例数据  
   
   
   
   
   
   
   
   
   
   
   
   
    X = np.array([[0, 0], [0, 1], [1, 0]])  
   
   
   
   
   
   
   
   
   
   
   
   
    y = np.array([-1, -1, 1, 1])  # 感知机通常使用+1和-1作为标签  
   
   
   
   
   
   
   
   
   
   
   
   
      
   
   
   
   
   
   
   
   
   
   
   
   
    # 创建并训练感知机  
   
   
   
   
   
   
   
   
   
   
   
   
    p = Perceptron(learning_rate=0.01, n_iters=1500)  
   
   
   
   
   
   
   
   
   
   
   
   
    p.fit(X, y)  
   
   
   
   
   
   
   
   
   
   
   
   
      
   
   
   
   
   
   
   
   
   
   
   
   
    # 因为原始数据使用-1和1作为标签，所以预测时需要将结果转换回-1和1  
   
   
   
   
   
   
   
   
   
   
   
   
    def convert_to_original_labels(y_predicted):  
   
   
   
   
   
   
   
   
   
   
   
   
        return np.where(y_predicted == 1, 1, -1)  
   
   
   
   
   
   
   
   
   
   
   
   
      
   
   
   
   
   
   
   
   
   
   
   
   
    print(p.weights)  
   
   
   
   
   
   
   
   
   
   
   
   
    testX = np.array([[1, 1], [0, 0]])  
   
   
   
   
   
   
   
   
   
   
   
   
    # 预测并转换标签  
   
   
   
   
   
   
   
   
   
   
   
   
    predictions = convert_to_original_labels(p.predict(testX))  
   
   
   
   
   
   
   
   
   
   
   
   
    print("Predictions:", predictions)

单层感知机存在的问题：

单层感知机可被用来区分线性可分数据，对于AND，OR，NOT等逻辑运算，单层感知机可以很好的工作；
对于XOR非线性数据，单层感知机无法满足要求；

1.3 多层感知机

由于单层感知机存在对应问题，对于非线性数据，于是人们提出了多层感知机，通过在感知机模型中增加若干隐藏层，增强神经网络的非线性表达能力，就会让神经网络具有更强拟合能力。

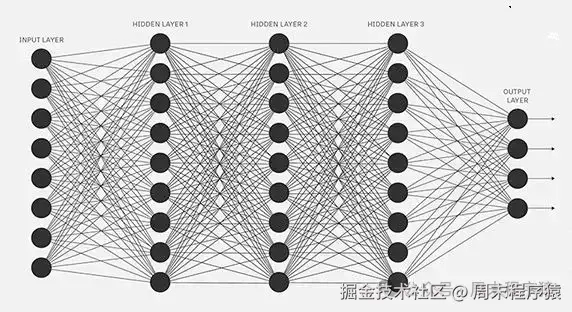
多层感知机

通过输入层、隐藏层和输出层，将神经网络分为三层：

输入层：负责接收输入数据，并传递给隐藏层，和单层感知机一样，接收多个信号；
隐藏层：相邻的神经元之间是全连接的，隐藏层接收输入层传递过来的信号，经过加权和运算后，传递给下一层；
输出层：负责接收隐藏层传递过来的信号，经过加权和运算后，输出一个结果；

通过numpy实现样例代码如下：

  
  
  
  
  
  
   
   
   
   
   
   
    import numpy as np  
   
   
   
   
   
   
   
   
   
   
   
   
      
   
   
   
   
   
   
   
   
   
   
   
   
    # 激活函数：Sigmoid  
   
   
   
   
   
   
   
   
   
   
   
   
    def sigmoid(x):  
   
   
   
   
   
   
   
   
   
   
   
   
        return 1 / (1 + np.exp(-x))  
   
   
   
   
   
   
   
   
   
   
   
   
      
   
   
   
   
   
   
   
   
   
   
   
   
    # 激活函数的导数  
   
   
   
   
   
   
   
   
   
   
   
   
    def sigmoid_derivative(x):  
   
   
   
   
   
   
   
   
   
   
   
   
        return x * (1.0 - x)  
   
   
   
   
   
   
   
   
   
   
   
   
      
   
   
   
   
   
   
   
   
   
   
   
   
    class MLP:  
   
   
   
   
   
   
   
   
   
   
   
   
        def __init__(self, input_size, hidden_size, output_size):  
   
   
   
   
   
   
   
   
   
   
   
   
            self.input_size = input_size  
   
   
   
   
   
   
   
   
   
   
   
   
            self.hidden_size = hidden_size  
   
   
   
   
   
   
   
   
   
   
   
   
            self.output_size = output_size  
   
   
   
   
   
   
   
   
   
   
   
   
            # 权重初始化  
   
   
   
   
   
   
   
   
   
   
   
   
            self.weights1 = np.random.randn(self.input_size, self.hidden_size)  
   
   
   
   
   
   
   
   
   
   
   
   
            self.weights2 = np.random.randn(self.hidden_size, self.output_size)  
   
   
   
   
   
   
   
   
   
   
   
   
      
   
   
   
   
   
   
   
   
   
   
   
   
        def feedforward(self, X):  
   
   
   
   
   
   
   
   
   
   
   
   
            # 输入层到隐藏层  
   
   
   
   
   
   
   
   
   
   
   
   
            self.hidden_input = np.dot(X, self.weights1)  
   
   
   
   
   
   
   
   
   
   
   
   
            self.hidden_output = sigmoid(self.hidden_input)  
   
   
   
   
   
   
   
   
   
   
   
   
            # 隐藏层到输出层  
   
   
   
   
   
   
   
   
   
   
   
   
            self.final_input = np.dot(self.hidden_output, self.weights2)  
   
   
   
   
   
   
   
   
   
   
   
   
            self.final_output = sigmoid(self.final_input)  
   
   
   
   
   
   
   
   
   
   
   
   
            return self.final_output  
   
   
   
   
   
   
   
   
   
   
   
   
      
   
   
   
   
   
   
   
   
   
   
   
   
        def backprop(self, X, y, output):  
   
   
   
   
   
   
   
   
   
   
   
   
            # 应用链式法则计算对权重的导数  
   
   
   
   
   
   
   
   
   
   
   
   
            d_weights2 = np.dot(self.hidden_output.T, (2*(y - output) * sigmoid_derivative(output)))  
   
   
   
   
   
   
   
   
   
   
   
   
            d_weights1 = np.dot(X.T, (np.dot(2*(y - output) * sigmoid_derivative(output), self.weights2.T) * sigmoid_derivative(self.hidden_output)))  
   
   
   
   
   
   
   
   
   
   
   
   
            # 更新权重  
   
   
   
   
   
   
   
   
   
   
   
   
            self.weights1 += d_weights1  
   
   
   
   
   
   
   
   
   
   
   
   
            self.weights2 += d_weights2  
   
   
   
   
   
   
   
   
   
   
   
   
      
   
   
   
   
   
   
   
   
   
   
   
   
        def train(self, X, y, epochs):  
   
   
   
   
   
   
   
   
   
   
   
   
            for i in range(epochs):  
   
   
   
   
   
   
   
   
   
   
   
   
                output = self.feedforward(X)  
   
   
   
   
   
   
   
   
   
   
   
   
                self.backprop(X, y, output)  
   
   
   
   
   
   
   
   
   
   
   
   
      
   
   
   
   
   
   
   
   
   
   
   
   
    # 示例：训练一个具有一个隐藏层的MLP（2输入，1隐藏层节点，1输出）  
   
   
   
   
   
   
   
   
   
   
   
   
    if __name__ == "__main__":  
   
   
   
   
   
   
   
   
   
   
   
   
        X = np.array([[0, 0], [0, 1], [1, 0]])  # 输入数据  
   
   
   
   
   
   
   
   
   
   
   
   
        y = np.array([[-1], [1], [1]])  # 目标输出（XOR函数）  
   
   
   
   
   
   
   
   
   
   
   
   
      
   
   
   
   
   
   
   
   
   
   
   
   
        mlp = MLP(2, 1, 1)  # 创建一个MLP实例  
   
   
   
   
   
   
   
   
   
   
   
   
        mlp.train(X, y, 1500)  # 训练MLP  
   
   
   
   
   
   
   
   
   
   
   
   
      
   
   
   
   
   
   
   
   
   
   
   
   
        print(mlp.weights1, mlp.weights2)  
   
   
   
   
   
   
   
   
   
   
   
   
        testX = np.array([[1, 1]])  
   
   
   
   
   
   
   
   
   
   
   
   
        print(mlp.feedforward(testX))  # 输出预测结果

1.4 距离和相似度

在机器学习中，距离计算是常用的方法，用于衡量两个样本之间的相似程度，这里把距离计算整理如下：

闵可夫斯基距离：d(x, y) = √[Σ|xi - yi|^p]^1/p，其中p=1时为曼哈顿，p=2时为欧式距离；
汉明距离：d(x, y) = Σ|xi 异或 yi|，在信息论中标识两个字符串之间对应位置的不同字符的个数；
KL散度：d(x, y) = Σ(xi * log(xi/yi))，KL散度是衡量两个分布之间的差异；

除了用距离标识对比相似性，还有通过相似度函数来做计算，如余弦相似度，皮尔逊相关系数，Jaccard相似系数等。

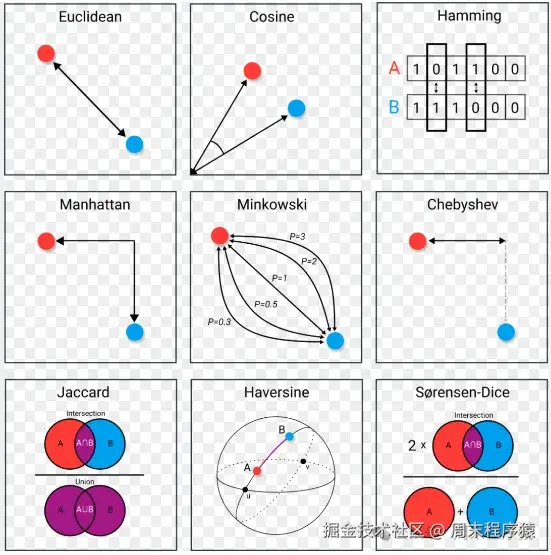
相似度比较

1.5 激活函数

激活函数是决定神经元是否传递信息的重要表达式单元，举例最简单的激活函数就是线性表达式：f(x) = a*x + b。

显然线性的表达式不能满足现实世界的需求，所以就出现了各种用于非线性变换的激活函数，常用的如下：

step：f(x) = {0, x<0; 1, x>=0} 只有两种状态，由于导数是0，无法用于神经网络；
sigmoid：f(z) = 1/(1 + e^-z)，Sigmoid函数的图像看起来像S形曲线，输出范围在0到1之间，并且连续；
双曲正切激活函数（Tanh）：f(z) = 2/(1 + e^-2z) - 1，Tanh和Sigmoid不同在于Tanh的输出范围在-1到1之间；
ReLu：f(z) = max(0, z)，ReLU函数在z<0时，输出为0，所以是一种线性激活函数，但是计算速度比较快，与之类似的还有Leaky ReLU；
ELU：f(z) = {z, x>0; a(e^z - 1), x<=0}，是为了解决ReLU的问题而提出的；
PReLU：f(zi) = {zi, zi>0; a*zi, zi<=0}，PReLU是ReLU的改进版，可以解决ReLU的梯度消失问题；
Softmax：用于多分类问题的激活函数，在之前的机器学习中也经常使用，其公式如下：e^z/Σ(e^zi)，Softmax的输出范围在0到1之间，并且连续；...

激活函数

以上是一些常用的激活函数，有兴趣可以自行查阅，这里不再赘述，不过引入另一个问题：

如何选择激活函数？

激活函数的选择对神经网络性能的影响很大，如果选择不合适，会导致梯度消失或者梯度爆炸；
梯度消失时候，避免使用sigmoid类似的函数，因为sigmoid函数的导数接近0；
神经网络中出现永不激活的神经元，优先使用PReLU；
ReLu函数只能在隐藏层使用，因为ReLu函数在输入小于0时，输出为0，导致梯度消失；
ReLu是通用的激活函数，可以在大多数情况下使用，如果没有找到最优解，再尝试其他的激活函数；

1.6 损失函数

损失函数是衡量模型预测结果和真实值之间的差异，损失函数越小，说明预测的结果越好，常用的损失函数如下：

均方误差（MSE）：E = 1/n * Σ(yi - y')^2，其中y'为预测值，常用于回归预测任务中；
交叉熵：两个概率分布之间的距离，旨在描绘通过概率分布 q 来表达概率分布 p 的困难程度；
Balanced L1 Loss：用于解决类似目标检测中的多任务的损失值计算的函数，分别计算分类损失和检测框损失；

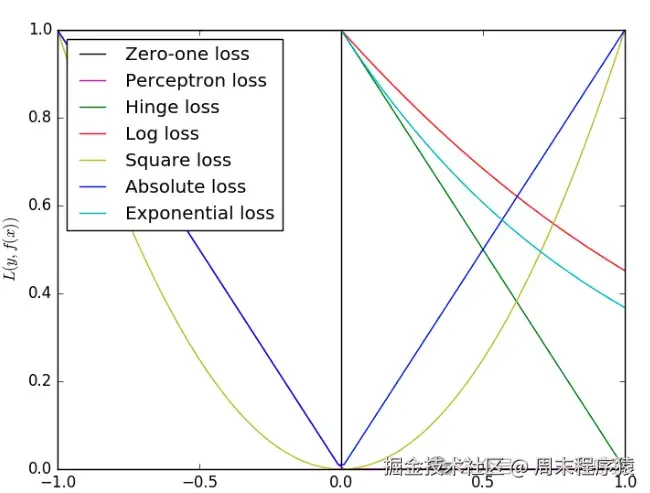
损失函数

2、评估指标

与通常的机器学习类似，深度学习也需要评估指标来衡量模型的性能，先整理一下机器学习常用评估指标。

常用的评估指标如下：

假设有这样一个表格：

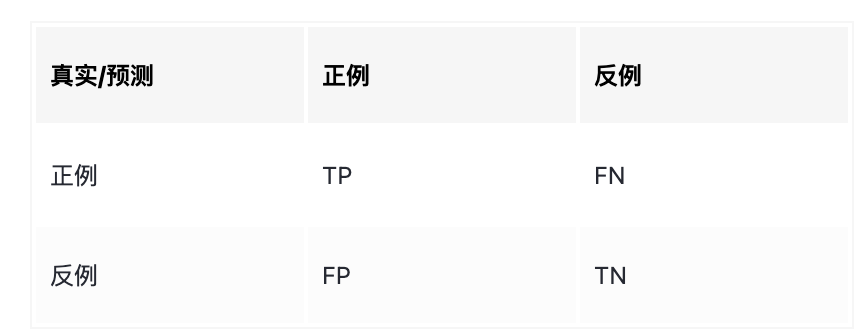
精度：acc = (TP + TN) / (TP + TN + FN + FP)，即所有分类正确的样本占所有结果样本的比例；
精确率（准确率）：prec = TP / (TP + FP)，即预测为正的样本中，真正为正的比例；
召回率：recall = TP / (TP + FN)，所有正样本中找出的比例；
P-R曲线：P-R曲线 = (P, R)，P表示召回率，R表示精确度，P-R曲线越接近左上角，说明模型性能越好；
F1值：F1 = 2 * prec * recall / (prec + recall)，综合精确度和召回率；
FPR值：FPR = FP / (FP + TN)，表示假阳性率；
TPR值：TPR = TP / (TP + FN)，表示真阳性率；
ROC曲线：ROC = (FPR, TPR)，FPR表示假阳性率，TPR表示真阳性率；

mAP指标

：

mAP常用于目标检测，衡量目标检测精度的常用指标，在计算mAP时，需要先算出准确率和召回率（上述的常用指标中有对应的计算方式），然后绘制P-R曲线，计算曲线下面积，这样就是AP值，最后将所有类的AP值求平均就是mAP。

举个例子：假设输入一张图有100个目标，预测得到90个目标，其中80个是正确的，4个是目标错误预测，20个是没有预测到的目标，那么准确率和召回率的计算如下：

准确率：acc = 80 / (80 + 4) = 95.2%；
召回率：recall = 80 / (80 + 20) = 80%；

3、归一化算法

什么是归一化，之前已经在机器学习部分介绍过，这里重新简单整理如下：

归一化：将数据映射到[0,1]之间，使数据分布均匀，也可以解决数据间的对比问题；
归一化方法：Min-max，Mean，Z-score，非线性归一等；
使用场景：Min-max，Mean一般适用于最大最小值明确不变的情况下，数据相对比较稳定，Z-score也可以称为标准化，会改变数据原来的属性，但是可以用于神经网络中，非线性归一化通常被用在数据分化程度较大的场景；

4、模型调优

4.1 学习率

什么是学习率，学习率是训练神经网络的超参数，代表每一次迭代中梯度向损失函数最优解的步长，由于学习率是找梯度，所以设置的大小都会影响收敛的速度；

学习率太小，收敛速度慢，容易陷入局部最优点；
学习率太大，收敛速度太慢，容易错过全局最优解；

为了解决以上设置的问题，在深度学习中会使用学习率衰减算法，比如分段常数衰减、指数衰减、自然指数衰减、多项式衰减、间隔衰减、多间隔衰减、逆时间衰减、Lambda衰减、余弦衰减、诺姆衰减、loss自适应衰减、线性学习率热身等，通过动态设置学习率，来保证收敛速度和精度；

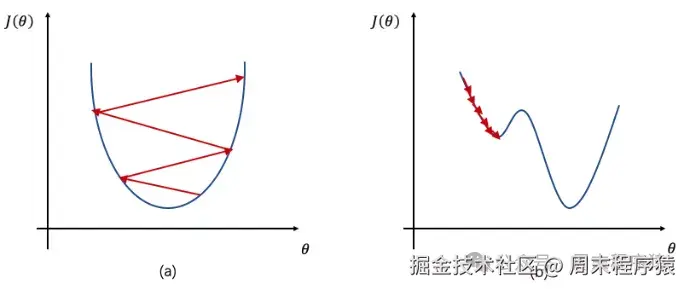
学习率

4.2 Batch Size

什么是Batch Size，在深度学习中，Batch Size是训练神经网络时一次迭代中样本的数量，可以是1到全体样本，一般是设置2的N次方；

为什么要有Batch Size这个超参数，在传统的梯度下降算法中，每次迭代都是整个训练数据进行计算，所以不需要Batch Size，但是深度学习算法中，由于数据量太大，为了找到全局最优解，通常不会使用传统梯度下降算法，而是通过mini-batch梯度下降算法，每次迭代中计算一部分数据，这样可以减少计算量，加快收敛速度；

Batch Size需要怎么设置？Batch Size设置越大，收敛速度越快，但是内存占用也越大，所以对于小样本可以直接设置和样本集一样大，对于数据量比较大情况下，建议从2-N进行验证，对比效果；

4.3 初始化参数

可以看到上面的 "单层感知机" 和 "多层感知机" 代码中，有一段是初始化

self.weights = np.random.random(n_features) * 2 - 1

权重，这是初始化参数的常用方法。

为什么要初始化参数，如果初始化参数为0或者固定参数，那么无论经过多少次网络训练，相同网络层内的参数值都是相同的，这会导致网络在学习时没有重点，对所有的特征处理相同，这很可能导致模型无法收敛训练失败。

4.4 正则化

什么是正则化？正则化是一种对学习算法稍加修改以使模型具有更好的泛化能力的技术，在深度学习中，正则化一般用于防止过拟合，减少模型对训练数据过度依赖的问题；

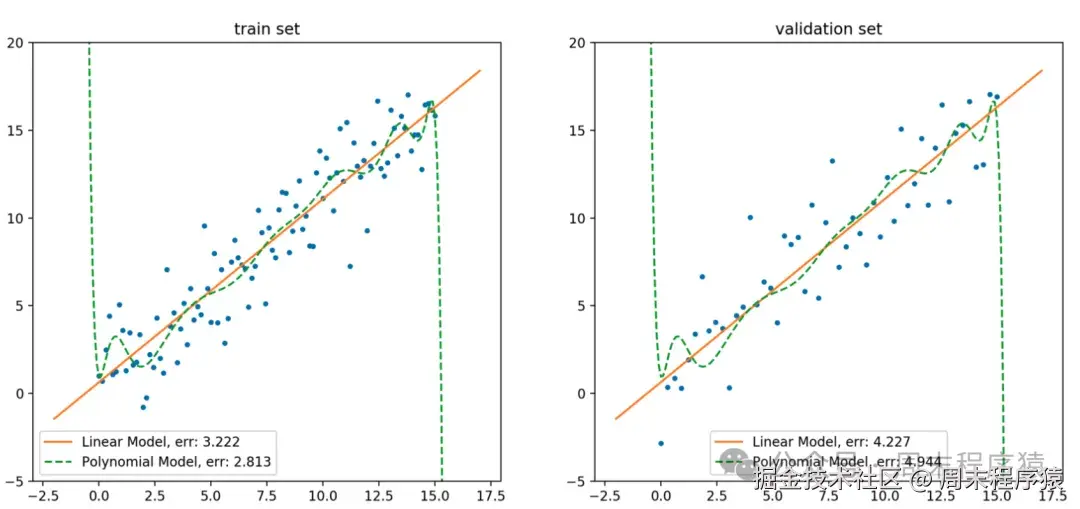
正则化拟合曲线

从上图中橙色直线是以线性模型拟合训练集数据得到模型的函数曲线，绿色虚线则是以15-阶多项式模型拟合训练数据得到模型的函数曲线。

由此可见，尽管多项式模型在训练集上的误差小于线性模型，但在验证集上的误差则显著大于线性模型，此外，多项式模型为了拟合噪声点，在噪声点附近进行了高曲率的弯折，这说明多项式模型过拟合了训练集数据。

怎么解决？

尽量减少选取变量的数量，从目标函数中选哪些特征变量比较重要，对于不重要的舍弃掉，对于重要的保留，这就是Dropout方法；
增加正则化项，对模型进行约束，让模型参数的取值尽量小，具体怎么做呢？由于前面的目标函数已经出现过拟合现象，所以我们需要尝试增加惩罚项，比如：
- 减少参数平方的总和，可以尝试对绝对值较大的权重予以很重的惩罚，绝对值很小的权重予以非常非常小的惩罚，这就是L2正则化；
- 保持参数的均方误差足够小，比如：f(x) = a + a1*x + a2*x^2 + a3*x^3 + a4*x^4中的a3和a4足够小，这就是L1正则化；

5、池化

什么是池化？池化是一种降采样方法，在深度学习中，池化通常用于减少特征数量，同时保留主要信息，比如对于一张图片100X100，通过2X2的窗口，缩小为50X50，保留主要信息，同时减少计算量；

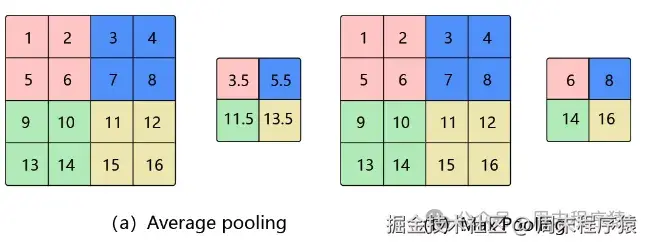
池化

池化的方法有很多，比如：平均池化、最大池化、K-max池化，其中平均池化就是求窗口内的均值，最大池化求窗口内的最大值，K-max池化是对窗口内的值进行排序，取前K个最大值；

通过pytorch实现样例代码如下：

  
  
  
  
  
  
   
   
   
   
   
   
    import torch
   
   
   
   
   
   
   
   
   
   
   
   
    import torch.nn as nn
   
   
   
   
   
   
   
   
   
   
   
   
    
   
   
   
   
   
   
   
   
   
   
   
   
    # 创建一个4x4的输入张量
   
   
   
   
   
   
   
   
   
   
   
   
    input_tensor = torch.tensor([[[[1, 2, 3, 4],
   
   
   
   
   
   
   
   
   
   
   
   
                                    [5, 6, 7, 8],
   
   
   
   
   
   
   
   
   
   
   
   
                                    [9, 10, 11, 12],
   
   
   
   
   
   
   
   
   
   
   
   
                                    [13, 14, 15, 16]]]], dtype=torch.float32)
   
   
   
   
   
   
   
   
   
   
   
   
    
   
   
   
   
   
   
   
   
   
   
   
   
    # 最大池化（Max Pooling）
   
   
   
   
   
   
   
   
   
   
   
   
    max_pooling = nn.MaxPool2d(kernel_size=2, stride=2)
   
   
   
   
   
   
   
   
   
   
   
   
    max_pooled_output = max_pooling(input_tensor)
   
   
   
   
   
   
   
   
   
   
   
   
    print("Max Pooled Output:")
   
   
   
   
   
   
   
   
   
   
   
   
    print(max_pooled_output)
   
   
   
   
   
   
   
   
   
   
   
   
    
   
   
   
   
   
   
   
   
   
   
   
   
    # 平均池化（Average Pooling）
   
   
   
   
   
   
   
   
   
   
   
   
    average_pooling = nn.AvgPool2d(kernel_size=2, stride=2)
   
   
   
   
   
   
   
   
   
   
   
   
    average_pooled_output = average_pooling(input_tensor)
   
   
   
   
   
   
   
   
   
   
   
   
    print("Average Pooled Output:")
   
   
   
   
   
   
   
   
   
   
   
   
    print(average_pooled_output)
   
   
   
   
   
   
   
   
   
   
   
   
    
   
   
   
   
   
   
   
   
   
   
   
   
    # 输出如下
   
   
   
   
   
   
   
   
   
   
   
   
    tensor([[[[ 6.,  8.],
   
   
   
   
   
   
   
   
   
   
   
   
              [14., 16.]]]])
   
   
   
   
   
   
   
   
   
   
   
   
    Average Pooled Output:
   
   
   
   
   
   
   
   
   
   
   
   
    tensor([[[[ 3.5000,  5.5000],
   
   
   
   
   
   
   
   
   
   
   
   
              [11.5000, 13.5000]]]])

参考

（1）paddlepedia.readthedocs.io/en/latest/t…

（2）www.cnblogs.com/jianxinzhou…

————————————————

原文链接：https://juejin.cn/post/7432964821056274468

如有侵权，请联系千帆社区进行删除