基于模仿学习的决策智能:大语言模型LLM会还原三阶魔方吗?
大模型开发/技术交流
- LLM
2024.09.24166看过
写在前面:本项目暂无任何实用价值,仅用于测试Transformer的学习能力。为了保证测试的合理性,建议在模型的推理过程中不使用任何基于搜索的算法,例如MCTS、BFS、DFS;不利用计算机的运算速度和存储记忆优势来搜寻较优解。
对于一个打乱的三阶魔方,很多人经过一段时间的训练可以快速还原,那人工智能可以达到或超过人的水平吗? 本文将通过训练一个会玩魔方的BERT分类模型来回答上述问题。
为什么选择BERT模型而不是GPT模型呢?我在《基于Transformer的决策智能》一文中发现BERT模型收敛更快。
先定义输出动作空间:
"U1", "U2", "U3", "R1", "R2", "R3","F1", "F2", "F3", "D1", "D2", "D3","L1", "L2", "L3", "B1", "B2", "B3",
U, R, F, D, L, B对应魔方的6个面:Up, Right, Front, Down, Left, Back。
1, 2, 3分别表示顺时针旋转90°, 180°, 270°
例如U1表示将Up面顺时针旋转90°,R3表示将Right面顺时针旋转270°(等效于逆时针旋转90°)
训练数据集比较简单,直接贴代码吧:
from random import SystemRandomrandom = SystemRandom()from torch.utils.data import Dataset"""https://github.com/hkociemba/RubiksCube-TwophaseSolverpip install RubikTwoPhase"""from twophase.cubie import CubieCube, moveCubeclass CubeDataset(Dataset):def __init__(self, alpha=1.2) -> None:self.weights = tuple([alpha**i for i in range(20)])self.population = tuple(range(1, 21))self.move_names = ["U1", "U2", "U3", "R1", "R2", "R3","F1", "F2", "F3", "D1", "D2", "D3","L1", "L2", "L3", "B1", "B2", "B3",]self.itos = ["-", " ", "\n","U", "R", "F", "D", "L", "B","0: ", "1: ", "2: ", "3: ", "4: ", "5: ",]self.face_names = ["U", "R", "F", "D", "L", "B"]self.stoi = {k:i for i, k in enumerate(self.itos)}self.color_id = self.stoi["U"]self.face_id = self.stoi["0: "]self.newline_id = self.stoi["\n"]self.space_id = self.stoi[" "]self.pad_id = self.stoi["-"]def reverse_move(self, m):m = int(m)m1 = (m // 3)m2 = (m % 3)m2 = 2 - m2return m1 * 3 + m2def __len__(self):return 1024 * 128def __getitem__(self, index):_ = index# n为随机打乱的步数,n越大,还原难度越高n = random.choices(population=self.population, weights=self.weights, k=1)[0]c = CubieCube()moves = []""" 随机打乱魔方,我们希望最小还原步数也为n,已发现:存在实际最小还原步数小于n的情况,暂时不知道如何解决例如以下几组都可以在更短的步数内还原打乱: U1 D1 F2 B2 U2 D1还原: D1 B2 F2 U1 D1--------------------------------打乱: R1 U2 L3 U2 L2 R3还原: L3 F2 L1 F2 L3--------------------------------打乱: B1 R1 L3 D2 R2 D2还原: R3 L1 B2 R2 B1--------------------------------打乱: B1 D2 B1 D2 B1 F1还原: B2 L2 B3 L2 F3--------------------------------打乱: U3 B2 U3 D1 L2 U3还原: L2 D3 U1 B2 U2--------------------------------打乱: D2 R2 F2 R2 U2 D3还原: D3 L2 B2 L2 U2--------------------------------打乱: F2 L2 F1 R2 F2 B3还原: B3 L2 F3 R2 B2"""for _ in range(n):while True:m = random.randrange(3*6)if len(moves) >= 1 and (moves[-1] // 3) == (m // 3): continueif len(moves) >= 2:f1 = self.face_names[moves[-2] // 3]f2 = self.face_names[moves[-1] // 3]f = self.face_names[m // 3]if f1+f2 in "UDU" and f in "UD": continueif f1+f2 in "LRL" and f in "LR": continueif f1+f2 in "FBF" and f in "FB": continuebreakc.multiply(moveCube[m])moves.append(m)fc = c.to_facelet_cube()aout = self.reverse_move(m)ain = []for i in range(54):if i % 9 == 0:ain.append(i//9 + self.face_id)ain.append(fc.f[i] + self.color_id)if (i+1) % 9 == 0:ain.append(self.newline_id)elif (i+1) % 3 == 0:ain.append(self.space_id)# 填充到固定长度ain += [self.pad_id] * 10return ain, aoutif __name__ == "__main__":c = CubeDataset()for _ in range(2):print()ain, aout = c[0]print("Input: ", len(ain))for e in ain:print(c.itos[e], end="")print()print("Label: ", c.move_names[aout])
训练样本示例如下:
Input: 880: FLF BUF LRD1: RDD URU LRD2: UBB LFB UDD3: BRF FDF BUL4: UDF FLD LLR5: RBR RBU BLU----------Label: U3Input: 880: FFF RUB BUB1: UDL RRF RDB2: RRL UFD LFD3: UUB BDF RLD4: RBU LLL UUF5: DLD RBB LDF----------Label: F1
说明:输入中U, R, F, D, L, B的具体含义可参考:
本文不做修改,仅添加编号、空格、换行等字符。魔方的初始状态为: UUUUUUUUURRRRRRRRRFFFFFFFFFDDDDDDDDDLLLLLLLLLBBBBBBBBB
经过n步随机打乱后,状态变为S,其中n小于等于20。对某个面旋转一次算一步,旋转90°, 180°, 270°都只算一步。
使用BERT分类模型,模型的输入为状态S,输出为还原魔方的下一步动作A。由于模型比较小,使用一张2G显存的显卡即可完成模型的训练。
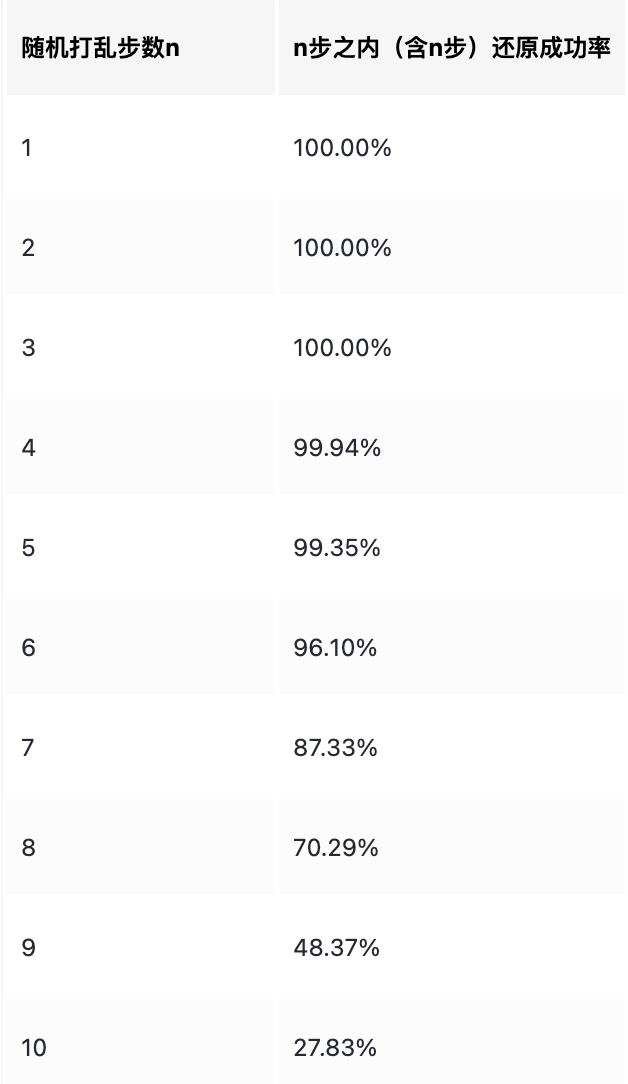
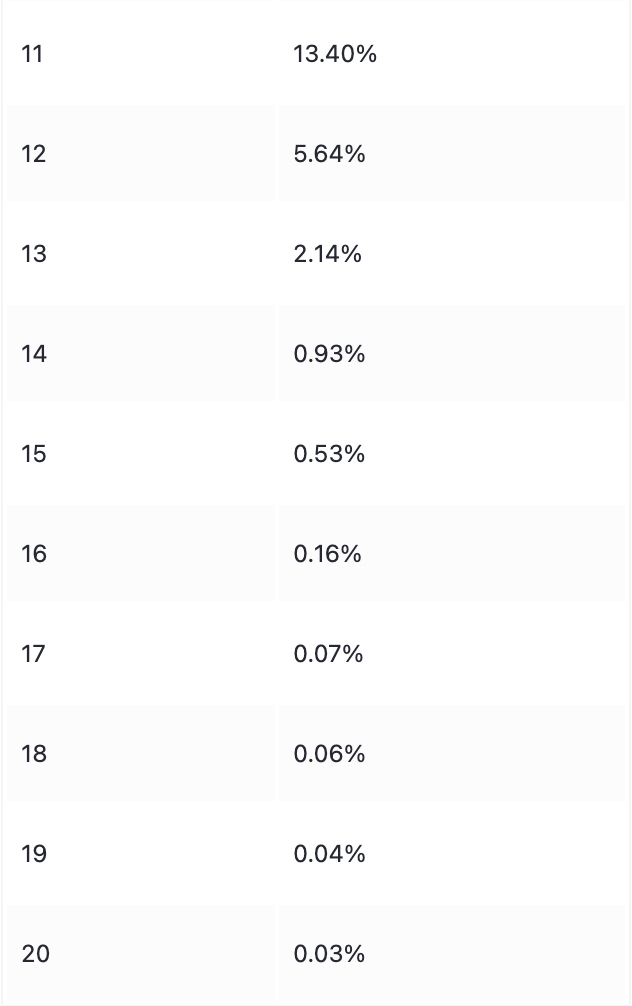
在测试环节,每次选择置信度最高的动作来还原魔方,若在n步之内(含n步)无法将魔方还原为初始状态,则失败。每轮测试10000次,统计成功率。
单卡训练约12小时,测试结果如下:
————————————————
版权声明:本文为稀土掘金博主「silicon」的原创文章
原文链接:https://juejin.cn/post/7381811719155105844
如有侵权,请联系千帆社区进行删除
写在前面:本项目暂无任何实用价值,仅用于测试Transformer的学习能力。为了保证测试的合理性,建议在模型的推理过程中不使用任何基于搜索的算法,例如MCTS、BFS、DFS;不利用计算机的运算速度和存储记忆优势来搜寻较优解。
对于一个打乱的三阶魔方,很多人经过一段时间的训练可以快速还原,那人工智能可以达到或超过人的水平吗? 本文将通过训练一个会玩魔方的BERT分类模型来回答上述问题。
先定义输出动作空间:
"U1", "U2", "U3", "R1", "R2", "R3","F1", "F2", "F3", "D1", "D2", "D3","L1", "L2", "L3", "B1", "B2", "B3",
U, R, F, D, L, B对应魔方的6个面:Up, Right, Front, Down, Left, Back。
1, 2, 3分别表示顺时针旋转90°, 180°, 270°
例如U1表示将Up面顺时针旋转90°,R3表示将Right面顺时针旋转270°(等效于逆时针旋转90°)
训练数据集比较简单,直接贴代码吧:
from random import SystemRandomrandom = SystemRandom()from torch.utils.data import Dataset"""https://github.com/hkociemba/RubiksCube-TwophaseSolverpip install RubikTwoPhase"""from twophase.cubie import CubieCube, moveCubeclass CubeDataset(Dataset):def __init__(self, alpha=1.2) -> None:self.weights = tuple([alpha**i for i in range(20)])self.population = tuple(range(1, 21))self.move_names = ["U1", "U2", "U3", "R1", "R2", "R3","F1", "F2", "F3", "D1", "D2", "D3","L1", "L2", "L3", "B1", "B2", "B3",]self.itos = ["-", " ", "\n","U", "R", "F", "D", "L", "B","0: ", "1: ", "2: ", "3: ", "4: ", "5: ",]self.face_names = ["U", "R", "F", "D", "L", "B"]self.stoi = {k:i for i, k in enumerate(self.itos)}self.color_id = self.stoi["U"]self.face_id = self.stoi["0: "]self.newline_id = self.stoi["\n"]self.space_id = self.stoi[" "]self.pad_id = self.stoi["-"]def reverse_move(self, m):m = int(m)m1 = (m // 3)m2 = (m % 3)m2 = 2 - m2return m1 * 3 + m2def __len__(self):return 1024 * 128def __getitem__(self, index):_ = index# n为随机打乱的步数,n越大,还原难度越高n = random.choices(population=self.population, weights=self.weights, k=1)[0]c = CubieCube()moves = []""" 随机打乱魔方,我们希望最小还原步数也为n,已发现:存在实际最小还原步数小于n的情况,暂时不知道如何解决例如以下几组都可以在更短的步数内还原打乱: U1 D1 F2 B2 U2 D1还原: D1 B2 F2 U1 D1--------------------------------打乱: R1 U2 L3 U2 L2 R3还原: L3 F2 L1 F2 L3--------------------------------打乱: B1 R1 L3 D2 R2 D2还原: R3 L1 B2 R2 B1--------------------------------打乱: B1 D2 B1 D2 B1 F1还原: B2 L2 B3 L2 F3--------------------------------打乱: U3 B2 U3 D1 L2 U3还原: L2 D3 U1 B2 U2--------------------------------打乱: D2 R2 F2 R2 U2 D3还原: D3 L2 B2 L2 U2--------------------------------打乱: F2 L2 F1 R2 F2 B3还原: B3 L2 F3 R2 B2"""for _ in range(n):while True:m = random.randrange(3*6)if len(moves) >= 1 and (moves[-1] // 3) == (m // 3): continueif len(moves) >= 2:f1 = self.face_names[moves[-2] // 3]f2 = self.face_names[moves[-1] // 3]f = self.face_names[m // 3]if f1+f2 in "UDU" and f in "UD": continueif f1+f2 in "LRL" and f in "LR": continueif f1+f2 in "FBF" and f in "FB": continuebreakc.multiply(moveCube[m])moves.append(m)fc = c.to_facelet_cube()aout = self.reverse_move(m)ain = []for i in range(54):if i % 9 == 0:ain.append(i//9 + self.face_id)ain.append(fc.f[i] + self.color_id)if (i+1) % 9 == 0:ain.append(self.newline_id)elif (i+1) % 3 == 0:ain.append(self.space_id)# 填充到固定长度ain += [self.pad_id] * 10return ain, aoutif __name__ == "__main__":c = CubeDataset()for _ in range(2):print()ain, aout = c[0]print("Input: ", len(ain))for e in ain:print(c.itos[e], end="")print()print("Label: ", c.move_names[aout])
训练样本示例如下:
Input: 880: FLF BUF LRD1: RDD URU LRD2: UBB LFB UDD3: BRF FDF BUL4: UDF FLD LLR5: RBR RBU BLU----------Label: U3Input: 880: FFF RUB BUB1: UDL RRF RDB2: RRL UFD LFD3: UUB BDF RLD4: RBU LLL UUF5: DLD RBB LDF----------Label: F1
说明:输入中U, R, F, D, L, B的具体含义可参考:
本文不做修改,仅添加编号、空格、换行等字符。魔方的初始状态为: UUUUUUUUURRRRRRRRRFFFFFFFFFDDDDDDDDDLLLLLLLLLBBBBBBBBB
经过n步随机打乱后,状态变为S,其中n小于等于20。对某个面旋转一次算一步,旋转90°, 180°, 270°都只算一步。
使用BERT分类模型,模型的输入为状态S,输出为还原魔方的下一步动作A。由于模型比较小,使用一张2G显存的显卡即可完成模型的训练。
在测试环节,每次选择置信度最高的动作来还原魔方,若在n步之内(含n步)无法将魔方还原为初始状态,则失败。每轮测试10000次,统计成功率。
单卡训练约12小时,测试结果如下:
评论
